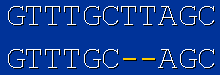Strings 2008 all
The Big Picture
Genomics has drastically changed the way we see the world
- Genome sequencing
- 1994 first (bacterial) genome sequenced
- 2001 Human genome completed
- ENCODE project (2007)
- Environmental surveys of life (2005-2007)
- 1000 Genomes program (2008)
- January 22 2008 NIH News: NIH announces "sequencing the genomes of at least a thousand people from around the world to create the most detailed and medically useful picture to date of human genetic variation"
- Creation of arteficial life
- 2008 synthetic Mycoplasma
- I am creating artificial life, declares US gene pioneer Article in The Guardian
- Move over Dolly. Synthia is on her way Article in The Economist
- 2008 synthetic Mycoplasma
Strings and searching
Why are we covering this material
- Strings are the most basic data structure to store information
- Strings are commonly encountered in all fields of daily life
- text strings (arts)
- bit or data strings (computer science, physics, astronomy, ...)
- biological sequences (biology)
- To retrieve information we need to search strings (quickly!)
- google text search
- search for extraterrestrial life
- searching genomic sequences
Topics in this section
- Background: Biological sequences
- What is DNA, RNA, protein
- The central dogma of biology
- Evolution (tree of life)
- Comparing sequences
- exact matches
- similar matches
- Searching pattern in sequences
- exact matches
- similar matches
Background: Biological sequences
- DNA, RNA, protein
- central dogma of molecular biology
- = transfer of sequence information from DNA (mastercopy) to RNA (blueprint) to protein (construct)
- introduce terminology: transcription and translation
- universal code of life (from tiny micro-organisms to large mammals)
- introduce the concepts of reading frames and reverse compliment
- evolution and tree of life
- discuss how organisms are related (evolution) and how this relations can be represented (tree of life)
Reading material:
Chapter 1 from Zvelebil and Baum's Understanding bioinformatics
Imtroduction to string comparison
A daily life task and key concept in science is comparing two objects. We learned earlier that a string is the simplest data structure to store information, thus by comparing two strings encoding the objects will allow us to compare them.
Examples:
- According to the Oxford English dictionary the correct spelling for the word is: Introduction. Was it spelled correctly in the title of this page?
- The DNA fragment ACTTTAGCCAT was extracted from a sample collected from the rare Babelfish. Further analysis has shown that the Babelfish sequence is ACTTGAGCCAT while the human sequence is ACTTTAGCCAT. Was the extracted DNA sequence indeed from the Babelfish or a contaminant of human DNA?
| Discovery question:
Go to Ensembl Human genome. How many base pairs does the human genome have? How long would it take you to compare the DNA of two humans if you can compare 10 nucleotides per second? |
Formalisation
Given two strings s1 and s2, compare each pair of elements. The two strings are the same if for all pairs the characters are identical.
simple python code
def StringsAreIdentical(s1, s2):
""" checks if two strings s1 and s2 are identical"""
# not identical if different length
if (len(s1) != len(s2)):
return 0
for i in range(len(s1)):
if (s1[i] != s2[i]):
return 0; # not identical
return 1
dna_probe = 'ACTTTAGCCAT'
dna_human = 'ACTTTAGCCAT'
dna_babelfish = 'ACTTGAGCCAT'
compare1 = StringsAreIdentical(dna_probe, dna_human)
compare2 = StringsAreIdentical(dna_probe, dna_babelfish)
if ((compare1 == 1) and (compare2 == 1)):
print "probe DNA is identical with both human and babelfish DNA"
elif ((compare1 == 1) and (compare2 == 0)):
print "probe DNA is identical with human DNA"
elif ((compare1 == 0) and (compare2 == 1)):
print "probe DNA is identical with babelfish DNA"
else:
print "probe DNA is identical with neither human nor babelfish DNA"
Pattern search
Text searching is an example of a simple problem with different algorithmic approaches. In practice most commonly one needs to check if a pattern (a short string) is contained in a larger string, and if so at which location.
Despite the simplicity of the problem, it is frequently used in bioinformatics. Examples:
- Find start (ATG) and stop (TAA, TGA and TGG) codons
- Find restriction enzyme cutting sites
- Search for PCR primer matches
Formalisation of the problem
Given a pattern p and a string s, find the first location where the pattern matches identically the string. Report the negative outcome if the pattern is not contained in the string.
The following sections describe basic search algorithms to locate a DNA fragment in a genome. But remember that the same concepts can be applied to any pattern/string pair. For further reading, the Wikipedia also has a good article on Text searching
Brute force (naive) search
The simplest, but also least efficient approach to text searching is to check whether the pattern matches the string at every possible position in the string. This is called the brute-force or naive string search algorithm. The procedure is illustrated below.
Simple python code
def naiveStringSearch(s, p):
"""native string search to find first occuranece of a pattern in a text"""
if (len(p) > len(s)):
return -1
for i in range(len(s)-len(p)+1): # all possible positions in text
match = 1
for j in range(len(p)): # all positions in pattern
if (s[i+j] != p[j]):
match = 0 # mis-match
if (match == 1):
return i
return -1
start = 'ATG'
dna = 'ATCGGCTAAATGGCTGCTATTAAGCT'
location = naiveStringSearch(dna, start)
print "The first start codon in the DNA sequence is at position %i" % (location+1)
Computational complexity
The runtime of the algorithm depends on both the length of the pattern and the length of the text string. If the text is n characters long and the pattern is m characters long, it takes O(n*m) computations.
| Discovery question:
Compare the runtimes of the naive string search algorithm with the python routine find in the string module. How does the string.find scale with pattern and text size? How do you think this is possible? |
Visual comparison of strings
Humans are very good at identifying patterns visually. One of the first ways to compare biological sequences was to generate identity matrices and visualise them in a so called dot plot.
Computing of a dot plot
The similarity between two sequences are represented by comparison matrix. Each element in the matrix compares the character in one sequence with the character of the other sequence. Identical character pairings are visualised by a black pixel while different characters are coloured white.
The table below illustrates an example of a dot plot comparing DNA fragments of hemoglobin from a person with sickle-cell disease and a healthy person. (This example can be generated interactively in class. It also is a nice example to show the effects of different mutations on the transcriptional outcome.)
| × | C | T | G | A | C | T | C | C | T | G | A | G | G | A | G | A | A | G | T | C | T | G | C | C |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | X | X | X | X | X | X | X | |||||||||||||||||
| T | X | X | X | X | X | X | ||||||||||||||||||
| G | X | X | X | X | X | X | X | |||||||||||||||||
| A | X | X | X | X | ||||||||||||||||||||
| C | X | X | X | X | X | X | X | |||||||||||||||||
| T | X | X | X | X | X | X | ||||||||||||||||||
| C | X | X | X | X | X | X | X | |||||||||||||||||
| C | X | X | X | X | X | X | X | |||||||||||||||||
| T | X | X | X | X | X | X | ||||||||||||||||||
| G | X | X | X | X | X | X | X | |||||||||||||||||
| T | X | X | X | X | ||||||||||||||||||||
| G | X | X | X | X | X | X | X | |||||||||||||||||
| G | X | X | X | X | X | X | X | |||||||||||||||||
| A | X | X | X | X | ||||||||||||||||||||
| G | X | X | X | X | X | X | X | |||||||||||||||||
| A | X | X | X | X | ||||||||||||||||||||
| A | X | X | X | X | ||||||||||||||||||||
| G | X | X | X | X | X | X | X | |||||||||||||||||
| T | X | X | X | X | X | X | ||||||||||||||||||
| C | X | X | X | X | X | X | X | |||||||||||||||||
| T | X | X | X | X | X | X | ||||||||||||||||||
| G | X | X | X | X | X | X | X | |||||||||||||||||
| C | X | X | X | X | X | X | X | |||||||||||||||||
| C | X | X | X | X | X | X | X |
Discovery questions:
|
Further (very advanced) reading for the Mathematics and Physics inclined
Recurrence plot of phase space trajectories
Similarity of sequences
In bioinformatic reality finding exact matches between sequences is not enough. Biological sequences may not be perfectly identical because of
- experimental errors that may have occurred in the determination of the sequence,
- mutations. Sequences may have changed in course of evolution
Further, biologist more often want to find other sequences that are similar to their sequence of interest rather then to re-identify identical sequences.
In the next sections we will explore how to compare and search for similar sequences.
How can sequences change (class room brain storming)
| Discovery question:
Imagine you have to type The quick brown fox jumps over the lazy dog 500 times on a type writer. What sort of changes in the text between the 500 versions are you likely to observe? Compare these changes with the changes you would expect comparing DNA sequences. |
How can biological sequences change?
1. Point mutation or substitution - one base replaced by another
2. "Indel"
2.1 Deletion - loss of one or more adjacent bases
2.2 Insertion - adding one or more bases
3. Large insertions or deletions
- Tandem repeats of genes
- Transposable elements
4. Recombination - crossover and gene conversion
(these are like cut-and-paste editing between two very similar texts)
Discovery questions:
|
For answer and examples see here
Evolutionary changes
- DNA sequences typically change very slowly
- e.g. 2*10-9 /base/year
- changes are not equally likely to persist everywhere
- some genomic regions may be mutated repeatedly while others remain unchanged.
- nucleotide changes are not equal likely
- Transitions (interchanges of purines (A⇔G) or of pyrimdines (C⇔T)) are more likely
- Transversions (interchanges between purines and pyrimdines) are less likely
(Image from: Mimicking Affinity Maturation)
Substitution matrices
Topcis
- What are substitution matrices
A substitution matrix is the mathematical form to describe the odds that a character changes into another character.
Discovery questions:
|
(Peter, is the concept of odds too hard and/or too confusing?)
odds = p / (1 - p), where p is the probability of the change. Thus the odds of the example above is 1/6, or what the bookmaker calls six-to-one.
- Why are odds used
Odds are used since we want to quantify how much *more likely* the change is compared to a random guess, and not how likely the change is.
Discovery questions:
|
- How to apply them in sequence comparison
When we compare biological sequences we generally assume that all characters change independently from each other. Under this assumption we then can compute the odds that one sequence changes into another by simply using the odds of each character change (or non-change) in each position of the two strings and multiplying all the odds together.
(Peter, are you comfortable with introducing log-odds here? Substitution matrices are really log-odd matrices and the values can be simply added together because of log(o1*o2*o3*..) = log(o1)+log(o2)+log(o3)...
The odds (log-odds) matrix (a.k.a. substitution matrix) of changing any character into any other character, provides us with a exactly quantifiable metric to compare two strings.
Illustration example (POD's comparing 4-5 students, and summarising the comparison in form of a tree).
Molecular based Tree of life
By comparing 1000s of character positions in molecular sequences accurate relationships between organisms can be established. Shown below is a phylogenetic tree computed from a universal gene present in in all living organisms.
POD, could you please help out with an example you'd like to present?
--ThomasHuber 11:42, 29 January 2008 (EST)